Abstract
Vaccine efficacy trials can often need large sample sizes as well as long follow-up times. The factors influencing the total trial duration are: vaccine efficacy and incidence, recruitment and lost-to-follow-up rates. At the planning stage assumptions on these factors are made to finalize the sample size. However, if the observed data in the target trial deviate from these assumptions then there is an increased risk of an under/over powered trial. We describe an efficient and flexible Bayesian trial design for testing for the vaccine efficacy of a new Tuberculosis (TB) vaccine in India. We first describe the Bayesian statistical framework and highlight key differences from the classical framework.
The Bayesian Statistical Framework
Unlike the traditional Frequentist framework, the Bayesian framework treats parameters of interest like Vaccine Efficacy (VE) as random (not fixed) and as such are assigned a probability distribution. Before the data is revealed, the chosen distribution is called the Prior which is then updated to the Posterior once the data is available using the Bayes Theorem. Todayβs posterior becomes tomorrowβs prior. All inference are then made using the posterior. When there is no a priori information on the parameters of interest then we assume a flat or a weakly-informative prior.
Consider vaccine efficacy (π πΈ). This is traditionally measured in terms of 1 - incidence rate ratio (vaccine vs. placebo) or as 1- hazard ratio. The latter is more efficient when anticipating long and varying follow-up times across study subjects. Another way to measure VE is in terms of the case proportion \[ (π = \frac{π_π£}{π_π£+π_π}) \] as \[ π πΈ = 100 Γ (1 β \frac{π_π£}{π_π}) = 100 Γ \frac{1β2π}{1βπ} \]
where ππ£ and ππ are the proportion of cases in the π£accine and πontrol arms respectively. The choice of such a parametrization facilitates sequential testing via multiple pre-specified interim looks. With large sample sizes and 1:1 randomisation, π can be estimates using \[ \frac {π_π£}{π_π£+π_π} \], where ππ£ and ππ are the observed number of cases. We present an adaptive and sequential vaccine efficacy trial design in the Bayesian framework and highlight important advantages. Testing a hypothesis of the form π»0 : ππΈ β€ 0.3 vs. π»π : ππΈ>0.3 would be equivalent to testing π»0 : π β₯ 0.411 vs. π»π : π<0.411. We will consider π as our parameter of interest (primary estimand) and assume a flat uniform prior (see Figure 1).
Statistical Significance (Success) Criteria: Once the target trial data is available, we update the prior to the posterior distribution using the Bayes Theorem. Since π is random, we can make probability statements about π or on any hypothesis regarding π based on the posterior. The trial would be deemed successful in showing efficacy (with a lower bound 30%) if Pr{π < 0.411 | π·} is high, i.e. the posterior probability of case-proportion being less than 0.411, given the data (π·), exceeds a high threshold (πΎ). For a fixed design (no interim looks) πΎ = 0.975 ensures a type-I error (πΌ) of 2.5% (one-sided). For an adaptive and sequential design like the one we propose, πΎ will need to be determined via simulations (under π»0).
Sequential Adaptive Design
- Initial Sample Size using the Frequentist log-rank test is around 148 cases required to reject π πΈ β€ 0.3 with 90% power at 2.5% πΌ-level (one-sided) if true (underlying) π πΈ = 0.6. β£ Assuming an incidence of 0.2/100 person-year (PY) in the first two years and 0.1/100 PY in subsequent years for the IGRA+ (TB infection test) cohort, a constant 0.1/100 PY for the IGRA- cohort, a 50-50 split between IGRA+/- and min. (max.) follow-up of 3(5) years, this would require around 42,000 subjects to be randomised. Sample size requirement will almost be halved if true VE = 0.7.
- Bayesian Design: To gain speed and to mitigate the risk of an underpowered trial due to uncertainty around VE, incidence, IGRA+/- split, etc. we propose a 7-look group sequential design:
β£ Plan for accruing a maximum of 140 cases and have 6-interim analyses (IA) starting at 80 cases and in increments of 10. The final look is at 140 cases.
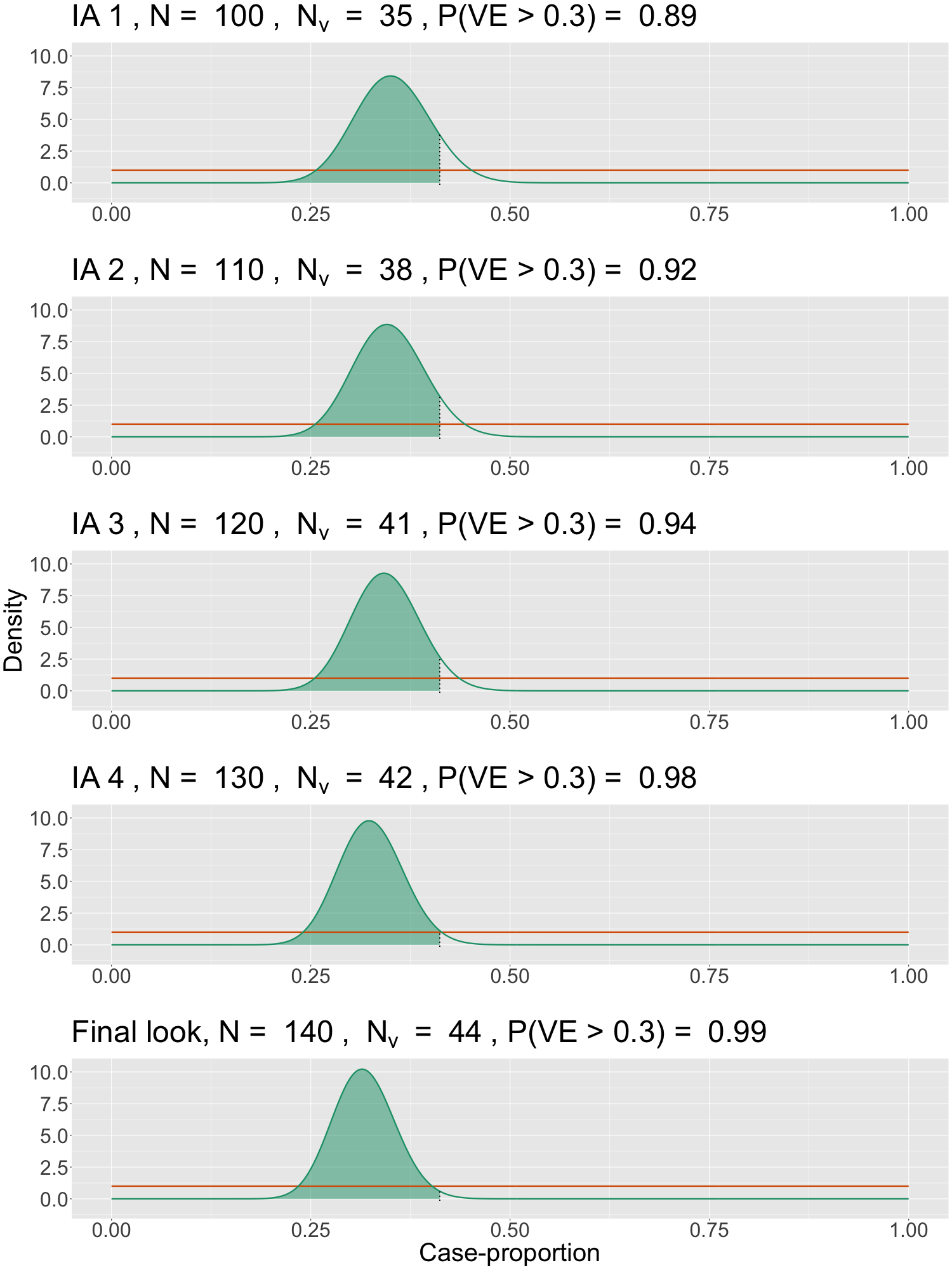
β£ Using alpha-spending approach, define varying thresholds πΎ1 β₯ πΎ2 β₯ β¦ β₯ πΎ7 β₯ 0.975 for the posterior probability of VE > 0.3 (equivalently, π < 0.411) computed at each look.
β£ Set πΎ-s above via simulations under the null scenario (π πΈ β€ 0.3): For type-I error of 2.5%, πΎπ = 0.997 for π = 1,2, πΎπ = 0.995 for π = 3,4,5,6 and for final πΎ7 = 0.98. Higher thresholds needed for interim stops. Figure 1, using simulated data, illustrates the sequential testing using posterior probabilities calculated at each interim and where the trial can be deemed successful only at the final look. Table 1 shows power and duration for sample sizes of 30K and 40K.
| N | Var./Cases -> | 80 | 90 | 100 | 110 | 120 | 130 | Final |
|---|---|---|---|---|---|---|---|---|
| 30000 | Power Duration |
0.46 4.5 |
0.61 5.0 |
0.74 5.4 |
0.83 5.9 |
0.86 6.4 |
0.91 6.6 |
0.96 7.5 |
| 40000 | Power Duration |
0.47 4.2 |
0.61 4.5 |
0.72 4.9 |
0.83 5.3 |
0.86 5.7 |
0.91 6.0 |
0.97 6.4 |
Advantages and Discussions
- Major advantage with the proposed Bayesian design is that it covers for VE between 0.6 and 0.7, with faster efficacy readout with higher VE.
β£ Relative to a traditional group sequential design, power/sample size advantage here comes from the ability to carry out sequential testing without the high alpha-spending that would be incurred in the traditional setting due to the reliance on the notion of extremism for calculating p-values.
β£ Use of case proportion as the primary estimand reduces data management burden and thus facilitates multiple interim looks. - Adaptive features like blinded sample size re-estimation and population enrichment (dropping IGRA-) can be easily incorporated into the design.
- Rigorous statistical and operational planning needed as well as early communication with the regulatory bodies for such innovative designs.