Bayesian Clinical Trial Designs for Rare Diseases

Abstract

The Bayesian statistical framework offers a flexible learn-to-confirm framework which allows for flexibility in designing clinical trials in the rare-disease space. It also works well for trials with small sample sizes. We introduce the Bayesian framework and touch upon some study design aspect that are relevant for trials in rare diseases.

A Simple Experiment

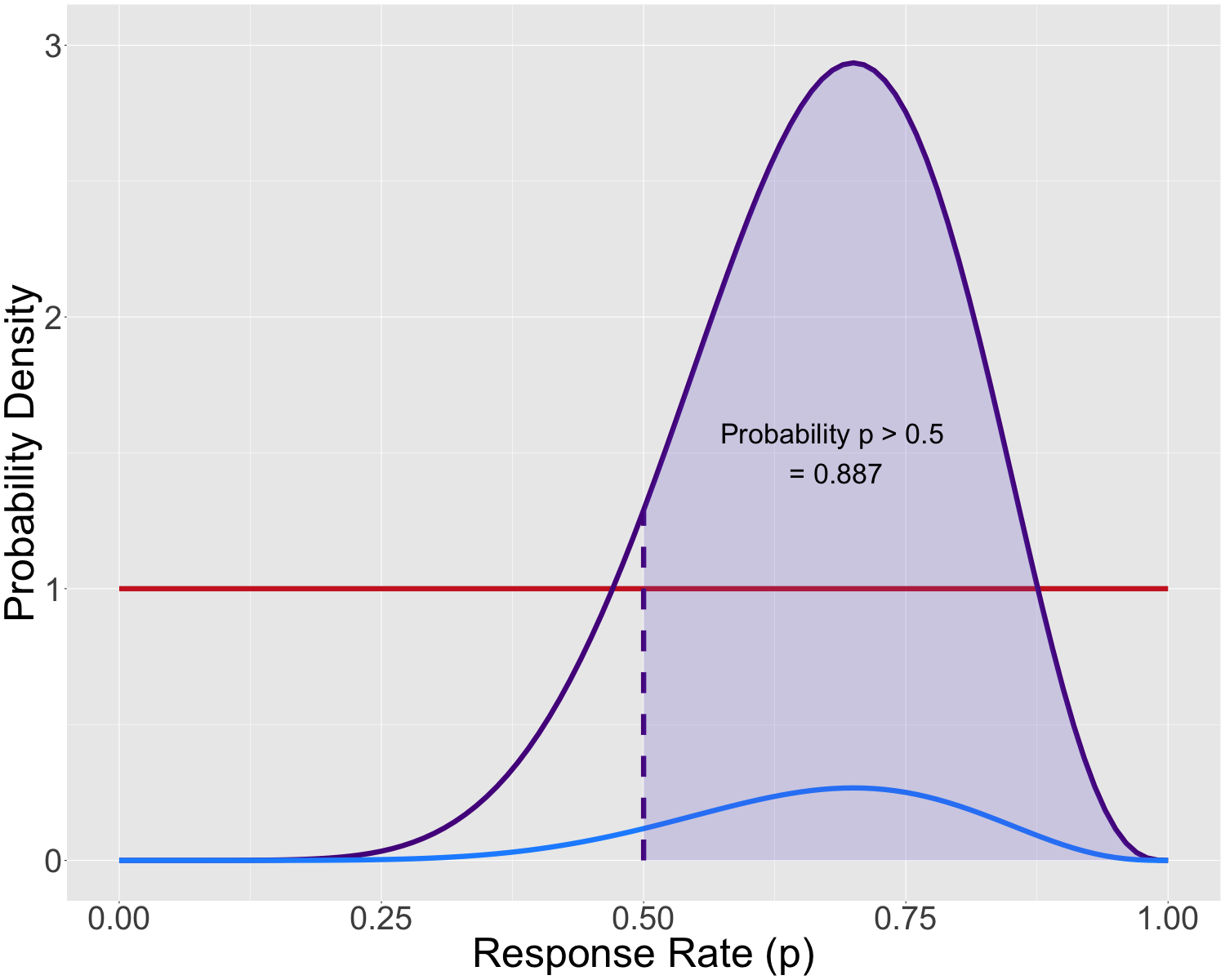
Suppose we treat 10 patients with a new drug and observe the no. with a particular response. Let the data be PPNNPPNPPN, (P: positive response; N: negative/no response). If the no. of trials (10) was pre-fixed then the experiment is Binomial of size 10. For testing the statistical hypothesis 𝐻0 : 𝑝 ≤ 0.5 vs. the alternative 𝐻𝐴 : 𝑝 > 0.5 (p: response rate) the p-value in the traditional (Frequentist) frame- work is 0.17 (not so extreme if the response rate 𝑝 was indeed 0.5) Now say we decide to add a stopping rule: Stop when 3 non-responses have been observed. This is the Negative-Binomial (NB) experiment. With the same data, we arrived at 10 trials for observing 3 non-responses. The p-value (computed using the NB distribution) for the same hypothesis test now is 0.02! So, what is happening here?
1. The definition of what is extreme is tied up to the definition of the experimental design;
2. The definition of what is extreme is under the assumption that the null hypothesis is true, i.e.𝑝=0.5. Thus fixing the value of the unknown parameter of interest.

The Bayesian Statistical Framework

Here the parameters of interest are treated as random (not fixed) and as such need to be assigned a probability distribution. Before the data is revealed, the assigned distribution is called the Prior which is then updated to the Posterior once the data is available using the Bayes Theorem. Today’s posterior becomes tomorrow’s prior. All inference are then made using the posterior. For the above example, starting with a flat prior (all values of 𝑝 equally likely between 0 and 1), the posterior prob- ability of 𝑝 > 0.5 is 0.887 regardless of the stopping rule being there or not. The inferential results are not tied up with the notion of extreme. As a result, adaptations can be done more reliably and without paying high statistical penalty (to preserve type-I error) for any data-driven changes to the future course of the trial. The Bayesian framework does not depend on large-sample theory, so, small N is well handled.

Figure 1: Prior (―), data likelihood (―) and the posterior (―).

Relevance to Rare Disease Trials

This opens up several adaptive and/or Learn-Confirm features that are very relevant for rare disease trials:
1. Inferentially seamless development from early to late phase, for example data-driven selection of hypothesis/endpoint, dose, population, etc. at an interim. Robust Go/No-Go and interim decisions can be made using Bayesian Predictive Probabilities such as probability of success at the end.
2. Adaptations for risk-mitigation like sample size re-estimation and population enrichment.
3. Flexible sample size: Sequential interim looks, stop trial when adequate evidence in favor or against the hypothesis has been obtained.
4. Bayesian borrowing of external/historical data such as a Single Arm trial or a trial with a small concurrent arm with augmented historical data via the use of an informative (not flat) prior for the control arm mean, response rate, etc.

A Case Study

• Phase-2/3 in rare chronic gastro. disorder with no approved treatment.
• Primaryendpointistheoccurrenceofmajorsymptoms(episodes)during the acute phase of treatment.
• Rate assumptions: SoC arm: 0.15; Low dose: 0.35; High dose: 0.4.
• Phase-2: Dose selection (Low/High); Phase-3: Efficacy confirmation
• Interim look at 40% of planned sample size. Planned sample size between 100 - 150, Maximum sample size between 150-180.

Bayesian Design (Using flat, non-informative priors)

• Simulations under the null (all arms rate 0.15) gives success criteria: $$\begin{gathered} Pr\{{𝑝}_{𝑠}-{𝑝}_{𝑐}<0 \\ | \\ 𝐷\}>0.98, \end{gathered}$$ i.e., given the data (𝐷), the occurrence rate in the 𝑠elected dose arm is lower than the 𝑐ontrol arm with a high probability. For this adaptive design, a probability threshold of 0.98 ensures a maximum type-I error of 2.5%.
• Interim decisions made using predictive probability of success(PPoS):
  ‣ If PPoS for both doses < 0.2 then consider futility (non-binding); OR
  ‣ If PPoS for both > 0.8 then choose low dose; OR
  ‣ Choose dose with higher PPoS. If 0.5 ≤ higher PPoS < 0.8 then consider increasing sample size.

Table 1: Sample Size and Power for Bayesian Adaptive Sequential Design.

Planned N	Max. N	Final Power (%)	High sel. (%)
100 120 120 120 140	150 150 160 170 180	79.0 84.8 85.6 86.6 89.1	58.5 57.1 56.4 59.8 56.3

• The same adaptive design in the traditional framework using inverse-normal combination and closed-testing for multiple comparisons has around 80% power with planned N = 140 and Max. N = 180. The prob- ability of correct dose selection is around 53%.
  ‣ Conservativeness comes from the use of the notion of extremism.

So what’s needed?

1. Careful and rigorous planning of such designs across phases.
   
2. Early communication with the Reg. bodies. Certain initiatives like the FDA’s Complex Innovative Design (CID) program encourage such designs for rare diseases with high unmet needs.
   
3. Frequentist design characteristics (Type-I,Power) need to be ascertained using simulations. Parallel computations can help with simulations for other types of endpoints that could be computationally more expensive compared to the binary endpoint discussed here.